La geometría del arte: cómo Da Vinci y Mondrian capturaron la matemática oculta en la naturaleza
En un nuevo estudio, se compararon las proporciones de varios árboles representados en obras de arte con los patrones de ramificación de los árboles reales
Los árboles representados en las obras de arte de pintores famosos como Leonardo da Vinci y Piet Mondrian siguen las matemáticas que subyacen al patrón de ramificación que se encuentra en los árboles reales, según afirma un nuevo estudio.
Según la investigación, publicada en la revista PNAS Nexus, esta matemática oculta en algunas pinturas abstractas podría incluso ser un factor intrínseco en nuestra capacidad para reconocer tales obras de arte como representaciones de árboles.
En la naturaleza, los árboles siguen un patrón de ramificación “autosimilar” denominado fractal, en el que las mismas estructuras se repiten a escalas cada vez más pequeñas desde el tronco hasta la punta de la rama.
En el nuevo estudio, los científicos examinaron matemáticamente la escala del grosor de las ramas en las representaciones de árboles en obras de arte.
Los investigadores derivaron reglas matemáticas para las proporciones entre los diámetros de las ramas y el número aproximado de ramas de diferentes diámetros.
“Analizamos los árboles en obras de arte como formas autosemejantes y fractales, y comparamos empíricamente el arte con las teorías sobre el grosor de las ramas desarrolladas en biología”, explicaron los investigadores.
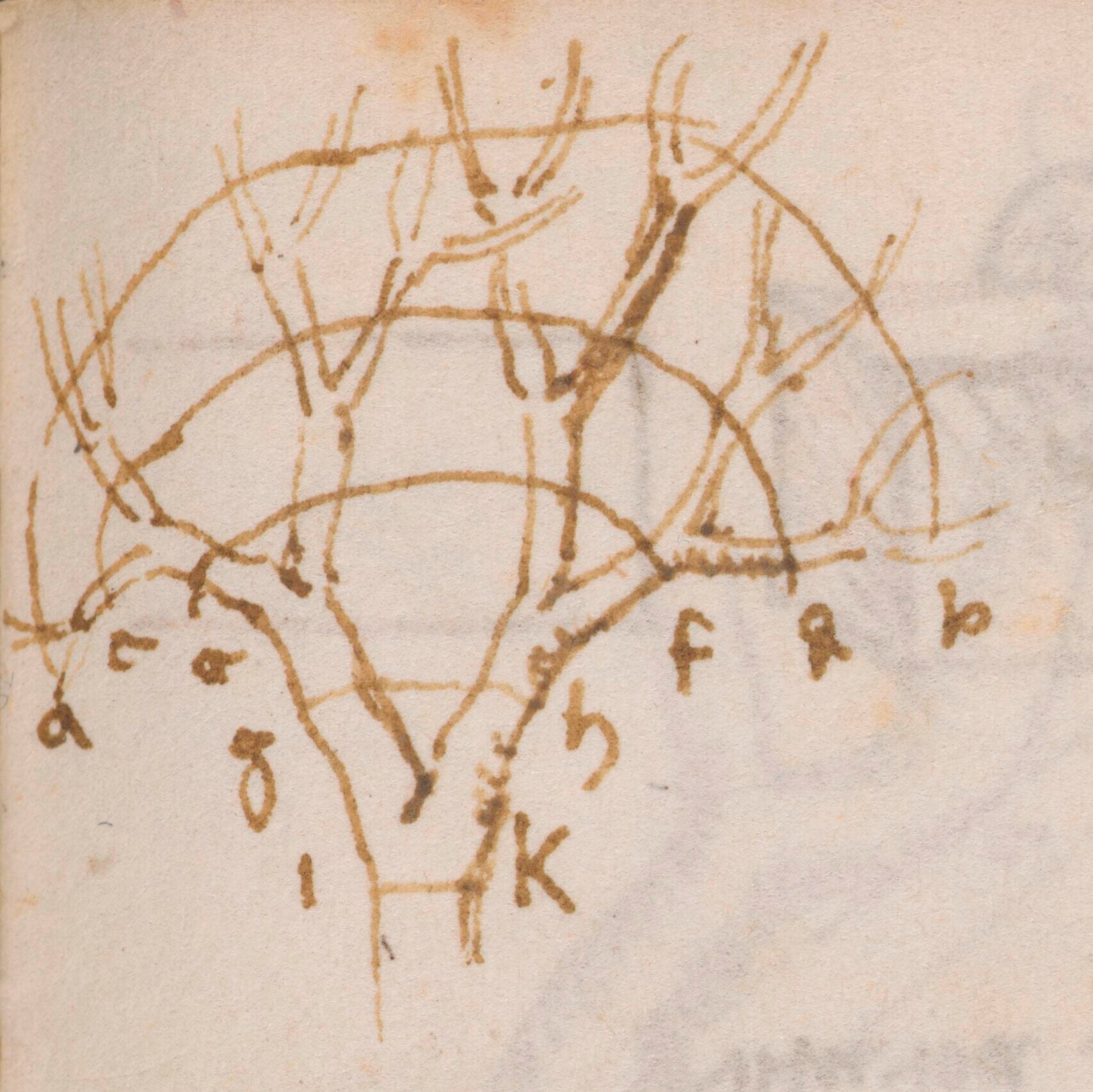
Leonardo da Vinci observó que las ramas de los árboles conservan su grosor al ramificarse.
El artista italiano del Renacimiento utilizó un parámetro llamado α para determinar las relaciones entre los diámetros de las distintas ramas.
Afirmó que si el grosor de una rama es el mismo que el grosor sumado de sus dos ramas más pequeñas, entonces el parámetro α sería 2.
Los investigadores analizaron árboles en obras de arte de varias partes del mundo, entre ellas las de la mezquita Sidi Saiyyed del siglo XVI en Ahmedabad (India), la pintura japonesa del periodo Edo y el arte abstracto del siglo XX.

Descubrieron que los valores de α en estas obras de arte oscilan entre 1,5 y 2,8, similar al rango de este valor en los árboles naturales.
“Aunque la dimensión fractal varía considerablemente entre árboles y obras de arte, observamos que el rango de α en los estudios de casos de grandes obras de arte a través de culturas y periodos de tiempo se corresponde con el rango de los árboles reales”, afirmaron.

Según los investigadores, incluso cuadros abstractos como el cubista Árbol gris, pintado por Piet Mondrian en 1912, que no muestra visualmente colores parecidos a los de un árbol, pueden identificarse como árboles si se utiliza un valor realista para α.
“Las pinturas abstractas con rangos α realistas son reconocibles como árboles, mientras que una pintura similar en otro sentido ya no es claramente reconocible como árbol”, afirman.
El nuevo estudio ofrece una perspectiva para “apreciar y recrear la belleza de los árboles”, afirman los científicos.
También pone de relieve que el arte y la ciencia pueden proporcionar visiones complementarias sobre los mundos natural y humano, añadieron.
Traducción de Sara Pignatiello






